When developing color grading tools, it’s common to engineer a function that takes a linear state image as input. It can be tempting to pre-compute these operations and bake them into a 33 or 65 point LUT to take advantage of the speedy application and cross platform nature of LUTs, but in this process is a mistake - the application of the LUT may substantially differ from the original function, even if all the samples within the LUT are accurate.

Cover photo: (Top Left) Image when encoded as Arri LogC3, this is the target that the others should aim to match. (Top Right) Same image, but the Linear to LogC3 function is a 129 point 1D LUT with a DOMAIN_MAX of 10. (Bottom Left) Linear to LogC3 function is a 65 point 1D LUT. (Bottom Right) Linear to LogC3 function is a 33 point 1D LUT.

The above image illustrates an image that I’ve transformed from ZLog2 to Arri LogC3, and three instances of differently sized LUTs used to capture the Linear to LogC3 portion of the log-to-linear-to-log pipeline. Evidently, the quality of this transform is very sensitive to the size of the LUT.

In the above example, the same LUT resolutions are used, but instead of using the LUT to capture the Linear to LogC3 function, the LUT is capturing the entire Z-Log2 to Arri LogC3 pipeline. Clearly, this result is much less sensitive to the LUT size.

By the end of this article, you should understand why the LUTs behave so poorly when designed to manipulate Linear state images.

• Theory
  • How do LUTs work?
  • Linear images
• Risks
  • Dynamic Range Clipping
    • Potential Solutions
  • Sampling Resolution
    • Potential Solutions
  • Takeaways:
• Example
  • Arri Linear to LogC3 vs 1D LUT
• Conclusion

Theory

How do LUTs work?

LUT is short for “look-up table”. Given a function \(f: \mathbb{R}^3 \rightarrow \mathbb{R}^3\) that takes an RGB value and outputs a new RGB value, a LUT evaluates \(f(r, g, b)\) at regular, evenly spaced intervals and stores each sample as an entry in a table. If the minimum and maximum input values specified by the DOMAIN_MIN and DOMAIN_MAX tags of the LUT are 0 and 1, then the first entry in the table will store \(f(0, 0, 0)\) and the last entry will store \(f(1, 1, 1)\). If the resolution of the LUT is \(N\), then a 1D LUT will have a table of \(N\) uniformly spaced samples of \(f(r = g = b)\)¹, and a 3D LUT will have \(N^3\) uniformly spaced samples of \(f(r, g, b)\).

When we want to apply the computed LUT to an image, we follow the following series of steps for each pixel’s code values \((r_i, g_i, b_i)\):

1. Each channel is clipped to the LUT’s specified input minimum and maximum allowed values - DOMAIN_MIN and DOMAIN_MAX
2. The nearest entries to \((r_i, g_i, b_i)\) in the table are identified
3. We interpolate between these nearest entries to estimate the value of \(f(r_i, g_i, b_i)\)

For further details, check out my writeup here

Linear images

An image is in a linear state if the code value of a pixel is directly proportional (\(f(x) = kx\)) to a quantity of light. This means that if one thing is a stop brighter than another, then it also has double the code value. For more details, check out my article here.

This differs from Log images, where the code value is roughly proportional to the logarithm of a quantity of light. Thus, every doubling in light results in a constant increase in the code value.

Risks

Given the above, there are generally two kinds of risks that come with LUTs on linear images. If these are not taken into consideration, the LUT will differ substantially from the function that it is meant to match.

Dynamic Range Clipping

The most obvious issue with a LUT is that it will clamp off any inputs that lie outside of the LUT’s domain. Any input RGB value that is lesser than the DOMAIN_MIN or greater than the DOMAIN_MAX will be clamped to that range before interpolation is conducted. If your linear image is scaled so that 0.18 corresponds to mid gray, then there will only be 2.47 stops² between mid gray and the default DOMAIN_MAX value for a LUT, 1.0. A log encoding can generally fit many more stops of highlight range between the mid gray value and the code value of 1.

Potential Solutions

To tackle this problem there are a few solutions:

1. Design the LUT so that DOMAIN_MAX is large enough to encapsulate your highlights
2. Gain the image down so that the brightest highlights lie at or below the code value of 1.0
3. Design the LUT to expect a log encoding that has enough highlight range below 1.0 so that your images are generally not clipped

Sampling Resolution

LUTs applied to linear images suffer from an inefficient allocation of samples. Most entries in the table will correspond to \(f(r, g, b)\) values where \((r, g, b)\) correspond to brighter parts of the image, and relatively few entries in the table will correspond to shadows. This is because the entries in the LUT are uniformly spaced with respect to code value, but the code value doubles with every stop of light.

To give a concrete example, suppose that we’re using a 1D LUT with a lut size of 9. It would then look something like this:

LUT_1D_SIZE 9
DOMAIN_MIN 0 0 0
DOMAIN_MAX 1 1 1

# placeholder values, the function would be evaluated at
# these code value and the result would be written in their place
f(0.000, 0.000, 0.000)
f(0.125, 0.125, 0.125)
f(0.250, 0.250, 0.250)
f(0.375, 0.375, 0.375)
f(0.500, 0.500, 0.500)
f(0.625, 0.625, 0.625)
f(0.750, 0.750, 0.750)
f(0.875, 0.875, 0.875)
f(1.000, 1.000, 1.000)

Let’s look at which entries would be used to interpolate between code values landing within each stop of light below DOMAIN_MAX:

You can therefore see that when the 1D LUT size was 9, then not every stop of light gets the same number of samples for interpolation. In the shadows (3+ stops below clipping), all inputs had to be determined from only the two neighbors: \(f(0.000, 0.000, 0.000)\) and \(f(0.125, 0.125, 0.125)\). The number of samples per stop of light decreased rapidly towards 2 as we went into the shadows.

If \(f(r, g, b)\) is not a linear function, then the linear interpolation between the two points would likely not follow the curvature of \(f\) and have substantial errors.

Obviously, a LUT Size of 9 is small, but increasing the resolution of the LUT only serves to change how many of stops of the linear image will receive a significant amount of samples to interpolate between. Each stop below DOMAIN_MAX will have about half as many samples to interpolate from, increasing the distance of the neighbors used for interpolation and therefore increasing the interpolation error for the shadows.

Potential Solutions

There are several approaches to this problem:

1. Use an enormous LUT size, so that the shadows you typically have are given a satisfactory quantity of samples. This only really works for 1D LUTs, where even 4096 samples is a reasonable file size. Because 3D LUT file sizes grow with the cube of the LUT resolution, they become enormous if you want a precise LUT.
2. Build the LUT to operate on log encoded images, so that each stop below the DOMAIN_MAX code value is given an approximately equal quantity of samples to interpolate between.

Takeaways:

Clearly, using a log encoding that is carefully selected to have enough highlight range to avoid clipping is the common solution to both of these problems. LUTs can be used on linear images, but unless you are carefully choosing your domain minimum and maximum and are using high resolution 1D LUTs, I would recommend against it.

Example

Arri Linear to LogC3 vs 1D LUT

Suppose we want to bake the Linear Scene Reflectance to Arri LogC3 function into a 1D LUT. If we want to cover the entire range of LogC3, we would then need to ensure that our DOMAIN_MAX is set to about 55, which maps to 1.0 in LogC3. I will deliberately use a 9 point LUT to make it so that the nature of the errors is visually obvious in the chart. A standard 9 point Linear to LogC3 1D LUT would look as below:

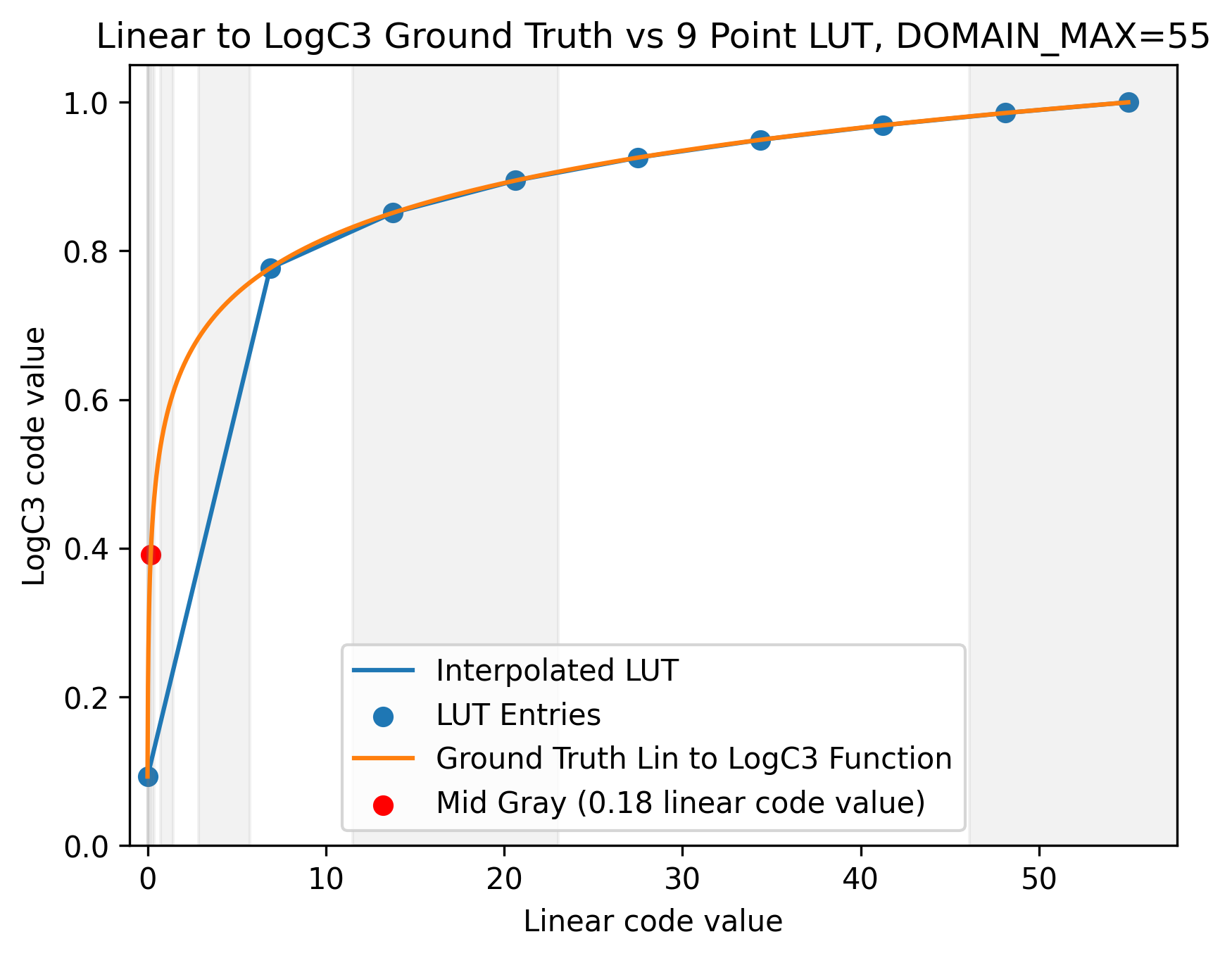
In the above graph, the samples in the LUT are placed uniformly with respect to the Linear code values. Each vertical stripe is one stop wide. Note that when the Linear to LogC3 curve is roughly linear between two points, the error is small. When the curvature is large, there is a large gap between the interpolated value and the ground truth function. Also note that most of the stops of dynamic range in this plot lie between the 0 and 5 marks. If we instead log scale the x-axis so that the shadows aren’t all crunched up on the left and so that each stop of light have a fixed width, we get the below plot:

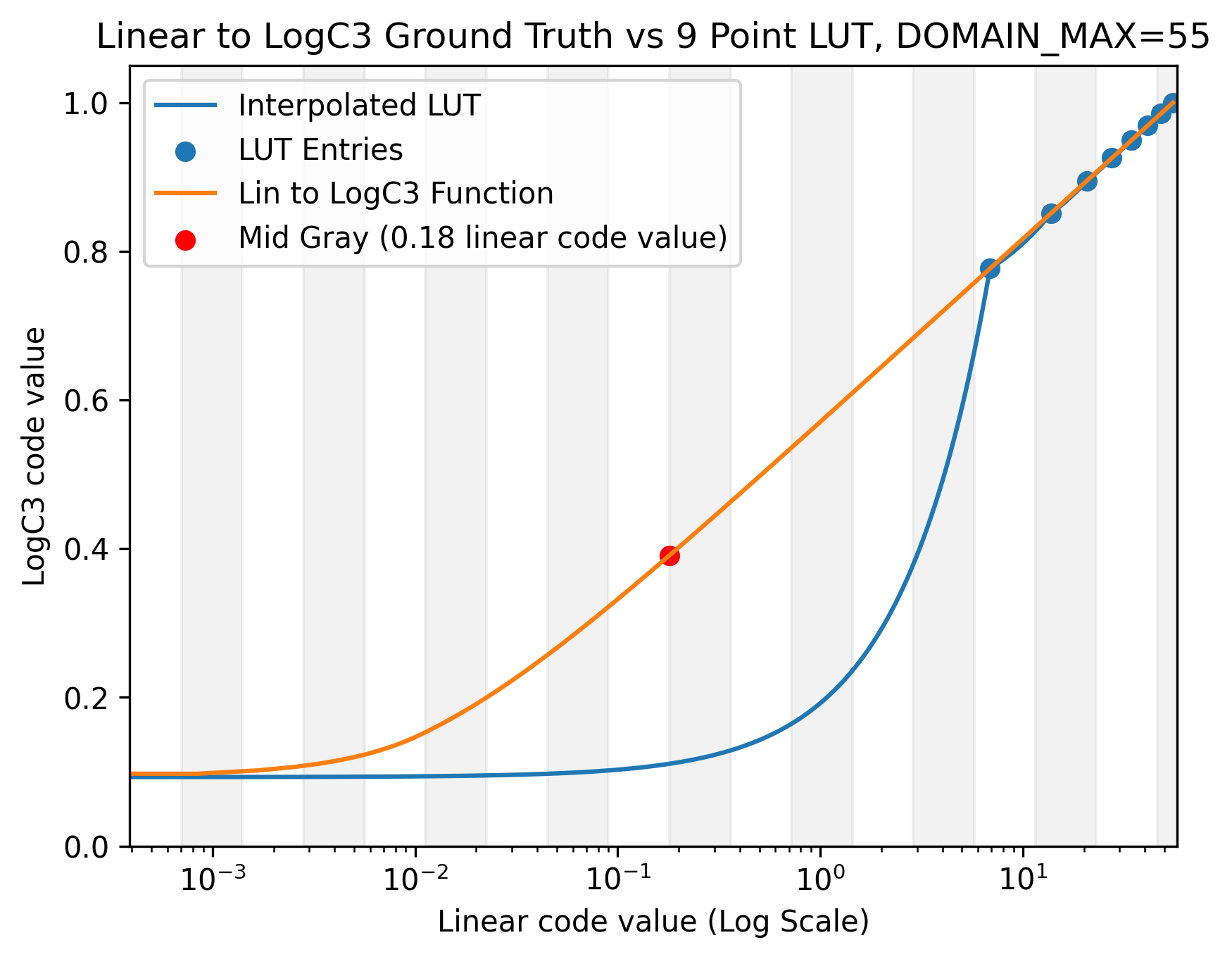
It should be clear that the majority of the LUT samples lie within the top three stops. This means that if an input code value is in the shadows, then the nearest entries in the LUT are far away and therefore the interpolation error is large, resulting in a big gap between the two curves.

Another approach we could leverage would be to sample uniformly with respect to the logarithm³⁴ of the linear image so you can handle negative inputs. This would allow for each pair of samples to have the same amount of stops of light between them. The above two charts are recreated with this scheme in mind:

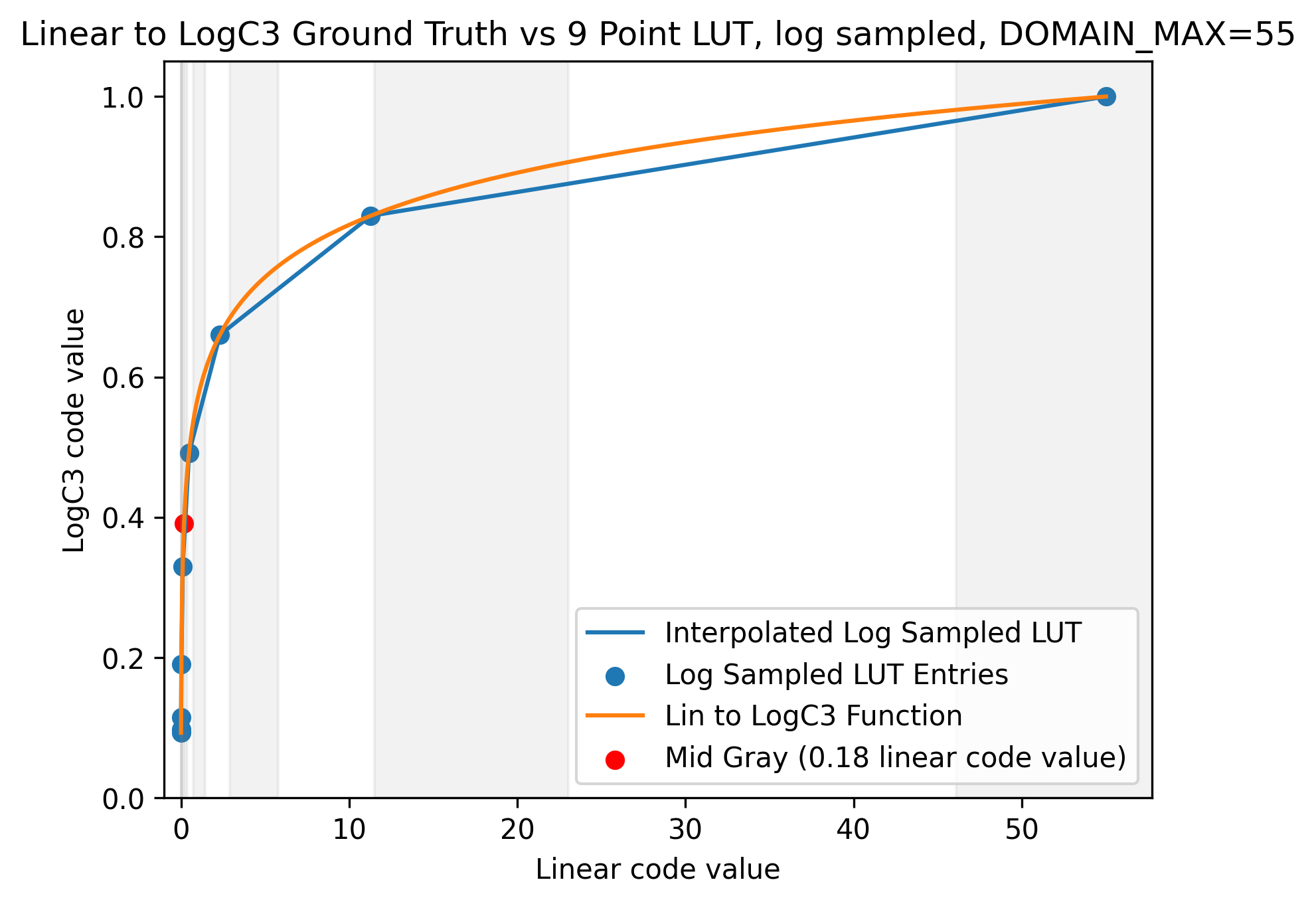
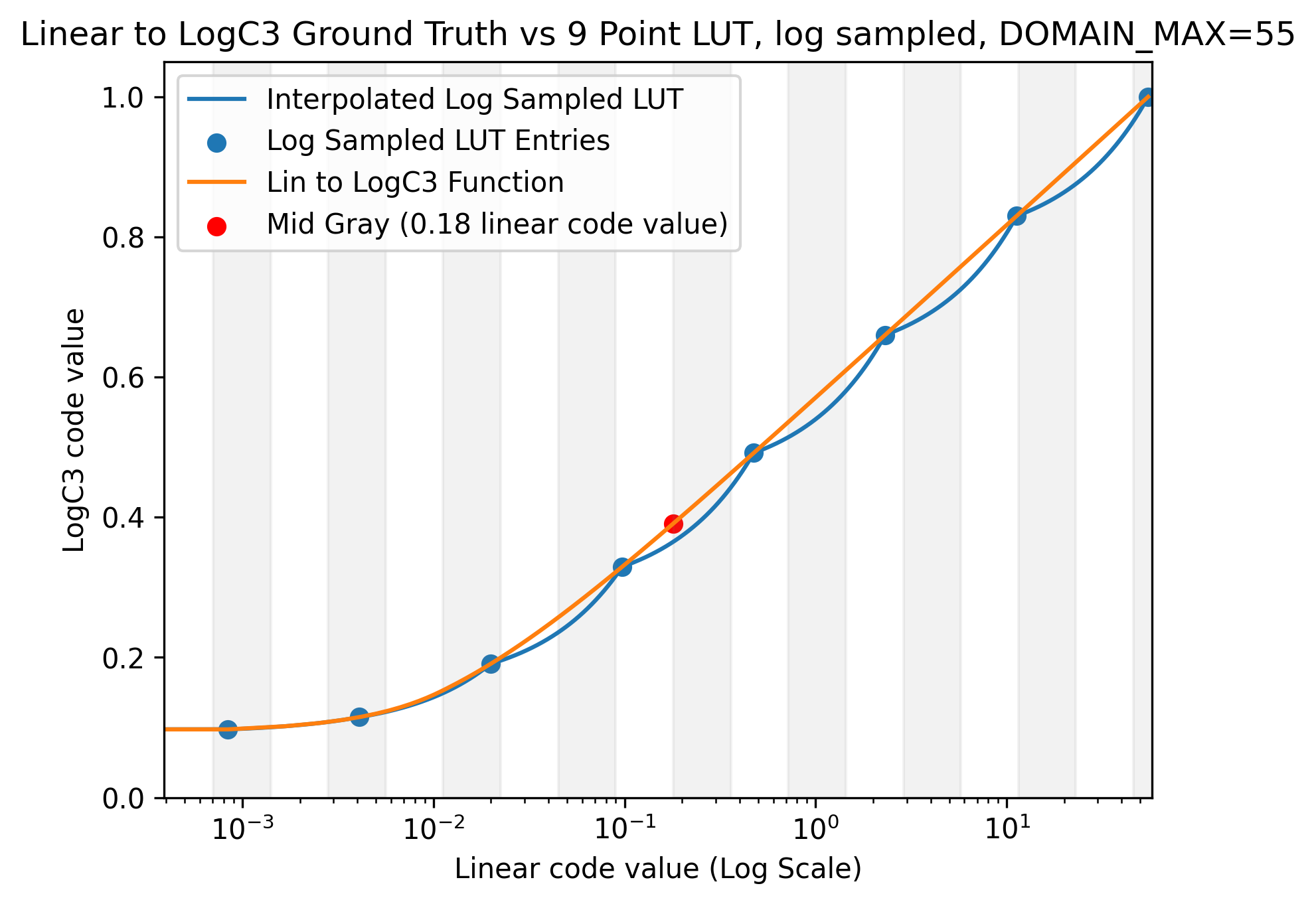
We can see that the error in the shadows of the Log vs Code Value plot is reduced. The remaining errors could be reduced further by increasing the LUT_SIZE to a more reasonable value.

Conclusion

Ultimately, 1D or 3D LUTs applied to a linear image will have reduced sampling resolution as the input code value falls many stops below the LUT’s DOMAIN_MAX value. When the nearest samples are farther away, the interpolation error is increased. This is a result of the uniform spacing of the LUT’s samples, which results in more samples in stops near DOMAIN_MAX and fewer in the shadow stops, when we would realistically want every stop of light to have a similar quantity of samples.

To attain this objective of making each stop of light have a similar quantity of samples, I recommend that one builds LUTs to take a log input, so that the uniform spacing of the LUT’s entries will all be spaced a similar amount of stops apart.